[Archive] Mathematics Teaching Exemplar–"The Sum of the first N Natural Numbers, the Squares of Natural Numbers and Cubes of Natural Numbers"

Programme Introduction:

Mathematics is a mode of thinking and an intelligence activity. It is not only a channel for effective communication, but also an avenue for learning other subjects. Gifted students with a high potential in Mathematics may not be contended with the regular Mathematics learning approach and content. They need a more flexible space for thinking, and a greater variety of challenging tasks to fully develop their outstanding talent. On the other hand, they also require assistance in cultivating their interpersonal skills to hasten their personal development.

With the help of some challenging mathematical tasks, gifted students can apply the knowledge acquired to discovering and exploring problems. Their higher-order thinking skills are thus cultivated and brought into full play. Considering the gifted students' learning needs, teachers have developed a pull-out Mathematics enhancement programme entitled "The Sum of the first N Natural Numbers, the Squares of Natural Numbers and Cubes of Natural Numbers". Following the students' immense interest in patterns and rules, teachers guide students to apply the concepts of patterns, rules and algebraic equations. Through a process of collaborative problem solving to deduce the formulae for "the sum of the first n natural numbers", "the sum of squares of n natural numbers" and "the sum of cubes of n natural numbers", students can acquire higher-level mathematical skills.

The above three sets of formulae fall within the scope of Stage IV learning. They are examples of Arithmetic Sequence, Geometric Sequence and its summation; whereas the application of the sign "å" is usually taught in the subject Additional Mathematics. In this programme, the students gifted in Mathematics are not only offered the opportunities to construct knowledge, to satisfy their desire to solve mathematic problems, to enhance their thinking, reasoning and explorative skills, they also learn to accept and understand others through collaboration.

Target: Secondary 1 to Secondary 3 students gifted in Mathematics

Objectives:

1. To enable students to work out the sum, sum of squares and sum of cubes of the first n natural numbers by guessing, verification and induction;
2. students can apply the knowledge acquired (i.e. the formulae of the sum, sum of squares and sum of cubes of the first n natural numbers) in problem solving;
3. to enhance students' higher-order thinking skill, and offer them opportunities to design inspiring mathematic questions;
4. to encourage students to apply mathematic thinking to solve problems encounter in everyday life; and
5. To cultivate their traits of tolerance and acceptance.

Learning and Teaching Process:

1. Teachers divide the programme into three interrelated teaching sessions ranging from elementary, intermediate to advanced level. The content compiles of "the sum of the first n natural numbers", "the sum of the squares and cubes of n natural numbers", and "extension courses".

    

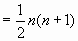2. To begin with, teachers may arouse the students' learning motive by raising a problem, such as "open my locker". Then, students are guided to deduce the formula for the sum of the first n natural numbers: 1 + 2 + 3 + … + n . By collaboration, the students are requested to work out tactics which can solve the mathematic problems developed from the above formula, e.g. If x = 1 + 2 + 3 + … + ( n - 1), solve x . Afterwards, they present their solutions to the entire class.

    

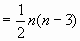3. When students are able to apply the above formula to a certain extent, teachers then give them some challenging tasks which include strategic thinking, applications in Mathematics and in everyday life. For example, the number of diagonal sides of n sided polygons . This training gives students more space to think, seek changes and innovate. Their thinking and problem-solving skills are also strengthened.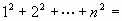

    

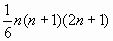4. Students are divided into groups, and each group selects the best piece of work from among its members. The authors of the selected works are asked to present them in front of the entire class, as a form of commendation.

    

5. Start by thinking about square numbers, students are guided to learn the "sum of the squares of the first n natural numbers" formula: . They are then given the chance to prove the formula for the volume of a cone by applying this formula (volume of a Cone 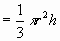) in the form of group collaboration.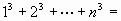

    

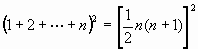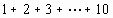
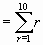6. Students are guided by questions about regular patterns toUsing some mathematical questions about regular patterns, students are guided to work out underlying patterns {e.g. 13 + 23 + 33 = 62, and 1 + 2 + 3 = 6；therefore, 13 + 23 + 33 + … + 3 = (1 + 2 + 3 + …. + n)2}. Moreover, they can apply their strong logical thinking skills to work out the formula for the sum of the cubes of the first n natural numbers: .

    

7. Teachers introduce a new mathematical expression to students: " å". For example, . Exercises involving the use of " å" enable students to explore its advantages. Afterwards, they are guided in applying another method to work out the formula for the sum of the squares of n natural numbers via group collaboration.

    

8. During discussions, students can share how they worked out the formula according to the requirements of Activities (4) and (6).

    

9. Teachers conduct a "Challenge the Difficulties" class activity to encourage the students' determination to succeed. Students are asked to discover "the sum of all numbers in the pyramid". They can work out the pattern of distribution (for example, the left-right balance in the distribution of numbers) only if they examine it carefully. Moreover, before they work out the formula for the sum of all numbers in the pyramid, they need to think about it in detail (for instance, 1 can be written as 12 x 1 = 13, and 2 + 4 + 2 can be written as 22 x 2 = 23). Using simplification strategies, the students finally realise this is another way to deduce the formula for "the sum of the cubes of first n natural numbers".

Learning Outcomes:

1. Throughout the entire learning and teaching process, teachers place equal emphasis on the students' thinking process, problem-solving methods and finding answers for the questions. The purposes of the activities are encouraging students' active participation, promoting self-learning and collaboration among students; enable them to enjoy trails, to face challenges and to be innovative. While the students are having fun in various thinking activities in Mathematics, they work out the following three formulae under the teachers' step-by-step guidance:

   • The formula for the sum of the first n natural numbers: 1 + 2 + 3 + … +

   • The sum of the squares of the first n natural numbers:

   • and the sum of the cubes of the first n natural numbers: .